Algoritmo de la Ruta Más Corta con Dijkstra | Explicación Gráfica

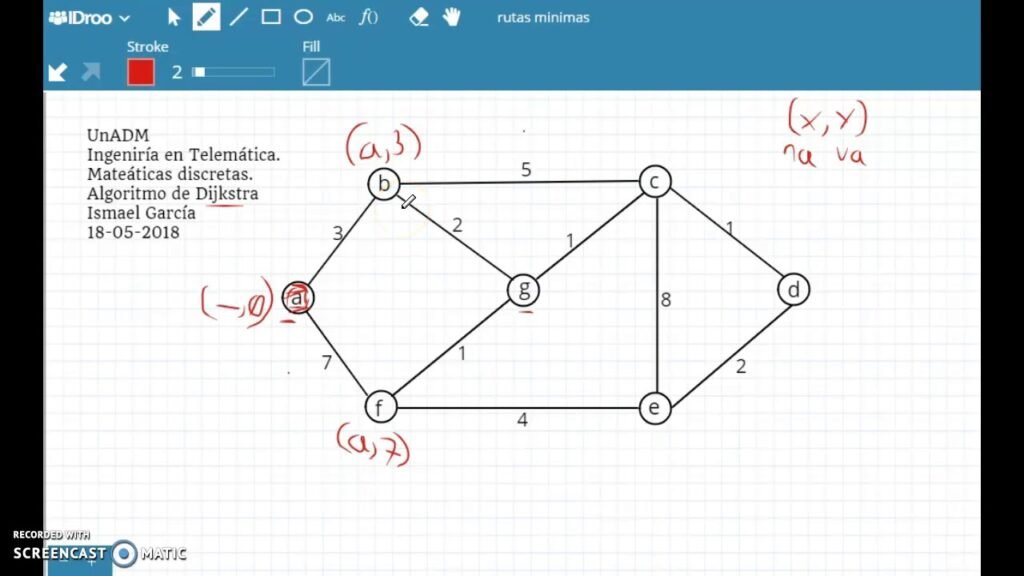
El Algoritmo Dijkstra, también conocido como Dijkstra Algoritmo, es una técnica usada para encontrar la ruta más corta entre dos puntos en un grafo. Este artículo va a explorar cómo funciona exactamente el Dijkstra y nos llevará paso a paso por un ejemplo gráfico para entender mejor este algoritmo.

¿Qué es el algoritmo de Dijkstra?

El algoritmo de Dijkstra, también conocido como simplemente Dijkstra en algunos círculos, es una técnica matemática utilizada para encontrar el camino más corto o ruta más rápida en un grafo (una estructura de datos que representa conexiones entre pares de elementos).

El algoritmo dijkstra, cuyo creador fue Edsger W. Dijkstra, se utiliza para encontrar el camino más corto desde un nodo (llamado el nodo de origen) hasta todos los otros nodos del grafo, creando así un árbol del camino más corto.

El dijkstra algoritmo tiene varias características clave: su propósito y uso son encontrar la ruta más corta en un grafo; fue inventado por Edsger W. Dijkstra; se aplica a grafos no dirigidos y ponderados (con valores asociados a cada arco); y es ampliamente usado en diversas industrias y dispositivos, como los GPS para encontrar el camino más corto entre la ubicación actual y el destino del usuario.

Características y requisitos del algoritmo

El Algoritmo Dijkstra tiene varias características clave que lo distinguen de otros métodos para encontrar la ruta más corta en un grafo.

Su propósito y uso son encontrar la ruta más corta en un grafo. Este es el principal beneficio de implementar este método.
La Ruta Más Corta con Dijkstra se usa ampliamente en diversas áreas, como la ingeniería civil para el diseño de sistemas de transporte y en sistemas informáticos.

El algoritmo de Dijkstra fue inventado por Edsger W. Dijkstra en aproximadamente 1959.

Historia y origen del algoritmo

El Dijkstra algoritmo fue inventado en 1959 por el ingeniero de software neerlandés Edsger W. Dijkstra, quien trabajaba en el Laboratorio Nacional de Física en los Países Bajos. En aquella época, Dijkstra estaba ocupado diseñando un sistema de control automático para los relojes del laboratorio.

Según se dice, la inspiración para crear el Dijkstra algoritmo llegó a Dijkstra mientras se preguntaba cómo podría ir en coche desde Rotterdam hasta Groningen. Esta pregunta cotidiana resultó ser la semilla que germinaría en algo mucho más grande: una solución innovadora y eficiente para encontrar caminos más cortos entre nodos en grafos, que pronto se convertiría en un componente fundamental en la programación computacional.

La invención del dijkstra algoritmo no solo revolucionó la forma en que los programadores abordaban los problemas de ruta más corta, sino que también demostró que las ideas innovadoras pueden surgir de situaciones cotidianas y simples.

Ejemplo gráfico paso a paso

En este ejemplo, vamos a aplicar el Algoritmo Dijkstra para encontrar la ruta más corta entre dos nodos en un grafo.

Paso 1: Inicialización

• Nuestro grafo es como sigue:

  A(10)-----B
  | /
  C--E

• El nodo de origen es A, y sus pesos son 10.

• Los otros nodos son B, C, D y E, con pesos desconocidos. Supongamos que los pesos entre el nodos son: AB = 2, BC = 4, CB = 3, CD = 5, DB = 1, DC = 6, AE = 10.

Paso 2: Dijkstra Algoritmo

• A: El costo desde A hasta sí mismo es 0, y el coste de ir desde A a cualquier otro nodo es mayor o igual al peso del camino más corto conocido desde A a ese nodo.

• En este caso, el costo mínimo para llegar al vértice B a través de su adyacencia directa con los vértices A es 10 (que es mayor que la suma de pesos entre B y C), por lo que nuestro vértice inicial será E (con un costo de ir desde A a él siendo de 10). Por tanto, el peso total para llegar al nodo E sería el mismo valor.

Algoritmo de la Ruta Más Corta con Dijkstra: fórmulas y cálculos

El Dijkstra Algoritmo es una técnica usada para encontrar el camino más corto o ruta más rápida en un grafo, que consta de nodos conectados por arcos. Este algoritmo fue inventado por Edsger W. Dijkstra.

Para aplicar el Algoritmo de Dijkstra, se sigue esta secuencia lógica de pasos: Seleccionamos un punto inicial (origen), y lo conectaremos con cada uno de los otros nodos del grafo a través del camino más corto.

El primer paso es identificar todos los nodos del grafo, así como sus respectivos costes o pesos. Una vez realizado esto, procedemos al siguiente paso en este tutorial, donde se presentan los pasos para aplicar el Dijkstra algoritmo y determinar la ruta más corta entre un origen y un destino.

Ventajas y limitaciones del algoritmo

El Dijkstra algoritmo, debido a su eficiencia y fácil implementación, ha demostrado ser una herramienta invaluable en la resolución de problemas de caminos más cortos. Una de sus principales ventajas es que puede manejar grafos con un gran número de nodos y arcos, lo cual lo hace ideal para aplicaciones donde la complejidad del problema es significativa.

La principal limitación del Dijkstra algoritmo es su incapacidad para encontrar caminos más cortos si los pesos de los arcos varían en el tiempo. Esto significa que debe re ejecutarse completamente cada vez que ocurre un cambio en la red, lo cual puede ser costoso en términos de recursos computacionales.

Aplicaciones reales del algoritmo en la vida real

El algoritmo de Dijkstra se aplica ampliamente en la industria, ya que proporciona una herramienta eficaz para determinar la ruta más corta entre dos puntos en un grafo. Un ejemplo común es el sistema de navegación por satélite (GPS), que utiliza el dijkstra algoritmo para encontrar el camino más rápido desde la ubicación actual hasta el destino deseo del usuario.

Además, el algoritmo Dijkstra se utiliza también en otras áreas como en los sistemas de planificación logística y transporte. Por ejemplo, en los sistemas de distribución de paquetes y en las empresas que ofrecen servicios de mensajería a demanda. El objetivo principal es encontrar la ruta más rápida posible para el vehículo o la entrega, minimizando así tiempos y costos.

Por otro lado, el algoritmo dijkstra también tiene aplicación en sistemas de información geográfica (GIS), donde se utiliza para determinar las distancias más cortas entre ciudades y localidades. Esto puede ser útil para planificar viajes y recorridos, tanto para personas como para vehículos.

El dijkstra algoritmo es una herramienta valiosa que encuentra diversas aplicaciones en la vida real, desde sistemas de navegación por satélite hasta la logística y transporte. Su capacidad para encontrar la ruta más rápida posible entre dos puntos ha revolucionado diversas industrias y mejorado la eficiencia en numerosas áreas.

Conclusión

El Algoritmo de Dijkstra, también conocido como el Dijkstra Algoritmo, es una herramienta poderosa para encontrar la ruta más corta en un grafo, especialmente cuando se enfrentan problemas complejos que requieren la optimización de rutas. El uso de este algoritmo permite a los desarrolladores y científicos resolver problemas complejos con eficiencia y precisión.

El Algoritmo Dijkstra ha demostrado ser una solución efectiva en múltiples áreas, como la planificación de rutas para dispositivos GPS, el manejo de redes y sistemas de información. Su capacidad para encontrar la ruta más corta entre dos puntos en un grafo lo convierte en una herramienta invaluable para resolver problemas de optimización.

El Dijkstra Algoritmo es una solución fundamentalmente práctica para encontrar rutas óptimas en grafos complejos.

Si quieres conocer otros artículos parecidos a Algoritmo de la Ruta Más Corta con Dijkstra | Explicación Gráfica puedes visitar la categoría Blog.