Notación Big O - Explicación con Ejemplos para Programadores

Si eres un programador, es posible que hayas escuchado hablar sobre la notación Big O, pero no te has detenido a pensar qué significa exactamente. En este artículo, vamos a explicar de manera sencilla y práctica qué es la Notación Big O y por qué es fundamental para cualquier desarrollador.

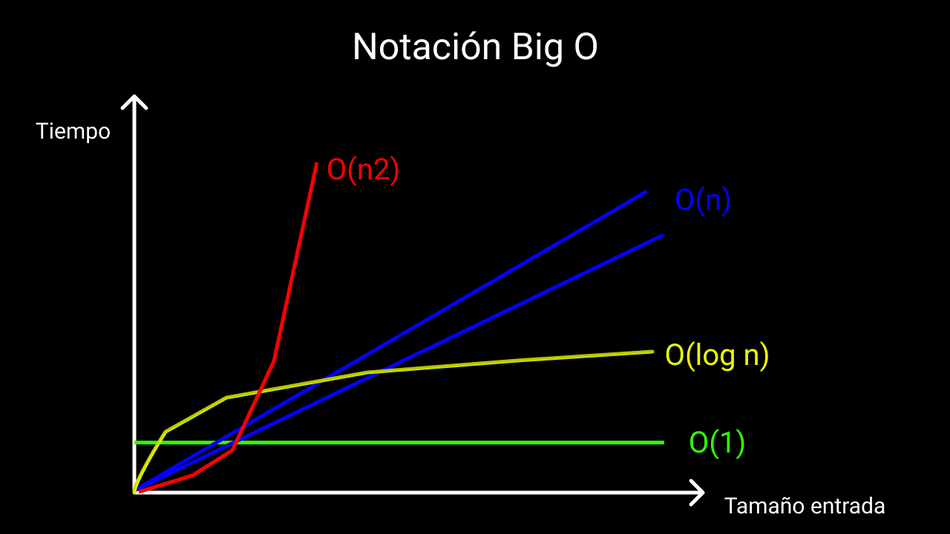
En el mundo de las programaciones, los algoritmos son fundamentales, y la complejidad de éstos puede ser muy importante. La Notación Big O es una forma de describir esta complejidad, indicando cómo cambia la cantidad de operaciones que un algoritmo realiza a medida que crece el tamaño del input.

¿Qué es la Notación Big O?

La notación big O se utiliza para describir el comportamiento de algoritmos y estructuras de datos en términos de su complejidad, siendo esta una medida de cómo crece el tiempo de ejecución con respecto a la cantidad de elementos del input.

En realidad, no hay una forma precisa para definir cuál es un buen o mal resultado. Sin embargo, la notación big O se enfoca en el peor caso, garantizando la complejidad máxima posible.

Cómo calcular la complejidad de un algoritmo

Cuando se trata de evaluar el rendimiento de un algoritmo, es crucial comprender su complejidad. La Big O Notation nos ayuda a hacer esto de manera eficiente y efectiva. Esta herramienta analiza el número de operaciones que realiza un algoritmo, permitiéndonos identificar patrones y comportamientos en función del tamaño del input.

Para calcular la complejidad de un algoritmo, debemos considerar dos conceptos clave: el peor caso y el promedio. El peor caso se refiere a la situación más crítica posible, donde las operaciones se realizan con mayor frecuencia y eficacia. En contraste, el promedio se enfoca en la ejecución del algoritmo en condiciones normales.

En términos de Big O Notation, podemos expresar la complejidad de un algoritmo como una función de su input. Por ejemplo, si un algoritmo tiene que procesar todos los elementos de una lista, su complejidad sería O(n), donde n es el número de elementos en la lista.

Ejemplos de Notaciones Big O comunes

La complejidad de algunos algoritmos es bastante fácil de comprender, como la búsqueda binaria. Esta técnica tiene una complejidad de O(log n) porque la cantidad de comparaciones que se realizan disminuye a medida que aumenta el tamaño del input.

El ordenamiento por selección también es un algoritmo simple y su complejidad es de O(n2), ya que para cada elemento del arreglo se necesita compararlo con todos los demás.

O(1) - constantes

La complejidad de O(1) es llamada constante porque el algoritmo tarda lo mismo en ejecutarse para cualquier input. Es decir, la función toma el mismo tiempo independientemente del tamaño del dato que le proporcionamos.

En términos prácticos, esto significa que hay una sola operación que siempre realizará el algoritmo, sin importar el número de elementos involucrados. Este tipo de funciones se usan comúnmente para acceder a datos en un índice específico y otras situaciones donde no hay mucho procesamiento.

La Notación Big O nos permite evaluar las complejidades de los algoritmos de manera rápida, evitando que dediquemos demasiado tiempo analizando el rendimiento del programa. Es especialmente útil cuando estamos implementando estructuras de datos o funciones para acceder a datos de forma eficiente.

O(log n) - búsqueda binaria

La notación big O notation es fundamental para comprender la complejidad de este algoritmo. La búsqueda binaria, por ejemplo, divide el rango de búsqueda en dos partes cada vez que compara un elemento con la media del conjunto.

Esta técnica permite encontrar elementos en un conjunto ordenado de manera eficiente. Algo que se destaca en esta notación es su capacidad para abordar situaciones específicas y aún así ofrecer una representación general de la complejidad del algoritmo.

O(n) - búsqueda simple

El caso de la búsqueda simple es un ejemplo común de complejidad lineal O(n), donde n es el número de elementos en la lista. Imagina que tienes una lista de alumnos en una clase y necesitas encontrar a alguien llamado María.

Si utilizas una búsqueda simple, mirarías cada elemento individualmente hasta encontrar al alumno, por lo que si la lista tiene 1000 estudiantes, la búsqueda tardaría igual de mucho que si tuviera solo 10.

O(n * log n) - ordenación rápida (Quicksort)

La ordenación rápida, también conocida como Quicksort, es un algoritmo de ordenamiento muy eficiente que se clasifica dentro del complejo de Notación Big O O(n * log n). Funciona eligiendo un elemento llamado pivote y distribuyendo a los demás elementos en dos subconjuntos según sean menores o mayores que el pivote. Después de eso, aplica la misma técnica a cada uno de estos subconjuntos para lograr una ordenación total.

O(n2) - ordenación por selección

El algoritmo de ordenación por selección tiene una complejidad de O(n^2), lo que significa que el número de operaciones es directamente proporcional a la cuadrática del tamaño del conjunto de datos.

Esta forma de ordenar implica seleccionar un elemento como "pivot" y luego compararlo con cada otro elemento en el conjunto para determinar su posición final. Sin embargo, esta aproximación puede no ser muy eficiente cuando los conjuntos de datos crecen, ya que requiere muchas operaciones adicionales al aumentar la cantidad de elementos.

Es importante tener en cuenta que aunque el big o notation es útil para evaluar y comparar diferentes algoritmos, no siempre refleja con precisión las condiciones prácticas del problema específico.

O(n!) - vendedor viajero

El problema del vendedor viajero es un clásico ejemplo de complejidad cúbica, que se puede expresar como O(n!). Este algoritmo implica encontrar la mejor ruta para recorrer todos los nodos (ciudades) en un grafo.
En el peor caso, este problema requiere intentarlo con cada uno de los n! rutas posibles.

Cómo comparar algoritmos utilizando la Notación Big O

La comprensión de cómo medir la complejidad de un algoritmo es crucial para tomar decisiones informadas sobre el desarrollo y mejora de software. La big o notation nos permite analizar y comparar los algoritmos, teniendo en cuenta su crecimiento en función del tamaño del input.

Algunas preguntas comunes a la hora de comparar algoritmos son:
"¿Cuál es el tiempo real necesario para que mi algoritmo termine?"
"¿Por qué algunas operaciones toman más tiempo que otras?"
En realidad, estas preguntas no se pueden responder directamente. Lo que sí podemos hacer es identificar la big o notation del algoritmo. Esto nos dará una idea de cuán rápida o lenta será en el peor de los casos.

Por ejemplo, si un algoritmo tarda 5 segundos para ordenar una lista de 100 elementos y otros 5 segundos para ordenar una lista de 1,000 elementos, podríamos concluir que el tiempo de ejecución aumenta linealmente con la cantidad de elementos. En este caso, la big o notation es O(n).

Ejemplos prácticos de Notación Big O en programación

En la práctica, la notación big O es utilizada para evaluar la complejidad de algoritmos y comparar su eficiencia.

O(1) - Constantes

El algoritmo que siempre realiza una operación fija, independientemente del tamaño del input, tiene una notación Big O de constante. Esto significa que el tiempo de ejecución es siempre igual para cualquier valor de input.

Por ejemplo:
python
def obtener_valor_constante():
return 5

La función anterior devuelve un valor fijo y no depende del tamaño del input, por lo que tiene una notación Big O de O(1).

O(log n) - Búsqueda binaria

La búsqueda binaria es un algoritmo eficiente para encontrar un elemento en una lista ordenada. Tiene una notación Big O de logarítmica, ya que el número de operaciones disminuye linealmente con la longitud de la lista.

Por ejemplo:
```python
def buscar_binario(lista, objetivo):
inferior = 0
superior = len(lista) - 1

while inferior <= superior:
    medio = (inferior + superior) // 2
    if lista[medio] == objetivo:
        return True
    elif lista[medio] < objetivo:
        inferior = medio + 1
    else:
        superior = medio - 1
return False

```
La función de búsqueda binaria reduce el tamaño del rango para buscar el elemento en cada iteración, por lo que tiene una notación Big O de O(log n).

Conclusión

La comprensión de la Notación Big O es crucial para cualquier desarrollador que desee crear algoritmos eficientes y escalables. Al conocer cómo evaluar y comparar diferentes implementaciones, puedes tomar decisiones informadas sobre qué opciones son las mejores para tus necesidades específicas.

Al aplicar la Notación Big O, puedes identificar patrones en tu código que pueden llevar a una mayor complejidad, y así poder optimizarlos. Esto no solo te ayudará a escribir más eficientemente tus algoritmos, sino también a mejorar el rendimiento general de tu aplicación.

Algunas veces la notación big o puede parecer abrumadora, pero con práctica y experiencia, puedes desarrollar una gran comprensión de cómo funciona y aplicarla en tus propios proyectos. Recuerda que cada pequeña mejora en la eficiencia del algoritmo puede tener un impacto significativo a largo plazo.

Si quieres conocer otros artículos parecidos a Notación Big O - Explicación con Ejemplos para Programadores puedes visitar la categoría Blog.